ielooki.blogg.se - Shading venn diagrams with 3 sets

SHADING VENN DIAGRAMS WITH 3 SETS FREE

Solution: It is given that 200 candidates scored above 90th percentile overall in CET. Question 4: If the number of candidates who are at or above the 90th percentile overall and also are at or above the 80th percentile in P in CET, is more than 100, how many candidates had to sit for the separate test for BIE? Altogether, there are 400 candidates this year who are at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Number of candidates below 80th percentile in P: Number of candidates below 80th percentile in C: Number of candidates below 80th percentile in M = 4:2:1.īIE uses a different process for selection. The same is the number of candidates at or above the 80th percentile only in M.Ĥ. The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. 150 are at or above the 80th percentile in exactly two sections.ģ. No one is below the 80th percentile in all 3 sections.Ģ. For the 200 candidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET:ġ.

Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. The test has three sections: Physics (P), Chemistry (C), and Maths (M). 54% of 500 = 270.ĭIRECTIONS for the question: Read the information given below and answer the question that follows.Īpplicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET).

The number of students who like watching at least two of the given games=(number of students who like watching only two of the games) +(number of students who like watching all the three games)= (12 + 13 + 14 + 15)% i.e.

The number of students who like watching only one of the three given games = (9% + 12% + 20%) of 500 = 205.

Ratio of the number of students who like only football to those who like only hockey = (9% of 500)/(12% of 500) = 9/12 = 3:4.Number of students who like watching all the three games = 15 % of 500 = 75.

Note: All values in the Venn diagram are in percentage. Now, make the Venn diagram as per the information given. N(B)= percentage of students who like watching basketball = 62% N(H) = percentage of students who like watching hockey = 53% N(F) = percentage of students who like watching football = 49%

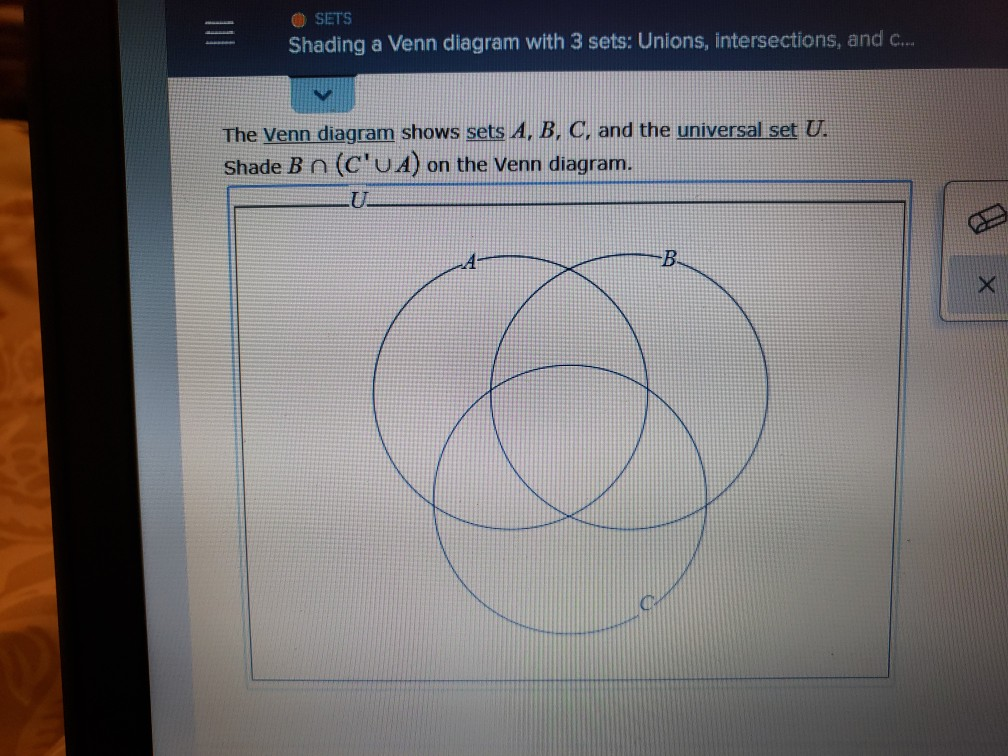
SHADING VENN DIAGRAMS WITH 3 SETS FREE

Kick start Your Preparations with FREE access to 25+ Mocks, 75+ Videos & 100+ Sectional/Area wise Tests Sign Up Now

Find the number of students who like watching at least two of the given games.

Find the number of students who like watching only one of the three given games.

Find the ratio of number of students who like watching only football to those who like watching only hockey.

How many students like watching all the three games?.

Also, 27% liked watching football and hockey both, 29% liked watching basketball and hockey both and 28% liked watching football and basket ball both.

Number of students who like at least one of tea or coffee = n (only Tea) + n (only coffee) + n (both Tea & coffee) = 60 + 40 + 80 = 180Įxample 2: In a survey of 500 students of a college, it was found that 49% liked watching football, 53% liked watching hockey and 62% liked watching basketball.

Number of students who like only one of tea or coffee = 60 + 40 = 100.

Number of students who like neither tea nor coffee = 20.

Number of students who like only coffee = 40.

Number of students who like only tea = 60.

Solution: The given information may be represented by the following Venn diagram, where T = tea and C = coffee.

How many students like at least one of the beverages?.

How many students like only one of tea or coffee?.

How many students like neither tea nor coffee?.

140 like tea, 120 like coffee and 80 like both tea and coffee. Solved ExamplesĮxample 1: In a college, 200 students are randomly selected. Tip: Always start filling values in the Venn diagram from the innermost value. W = number of elements that belong to none of the sets A, B or C